7-2. Small Sample Estimation of a Population Mean

The confidence interval formulas in the previous section are based on the Central Limit Theorem, the statement that for large samples $\bar{X}$ is normally distributed with mean $μ$ and standard deviation $σ/\sqrt{n}$ . When the population mean $μ$ is estimated with a small sample ( $n < 30$ ), the Central Limit Theorem does not apply. In order to proceed we assume that the numerical population from which the sample is taken has a normal distribution to begin with. If this condition is satisfied then when the population standard deviation σ is known the old formula $\bar{x}±z_{α∕2}(σ/\sqrt{n})$ can still be used to construct a $100(1−α)\%$ confidence interval for $μ$ .

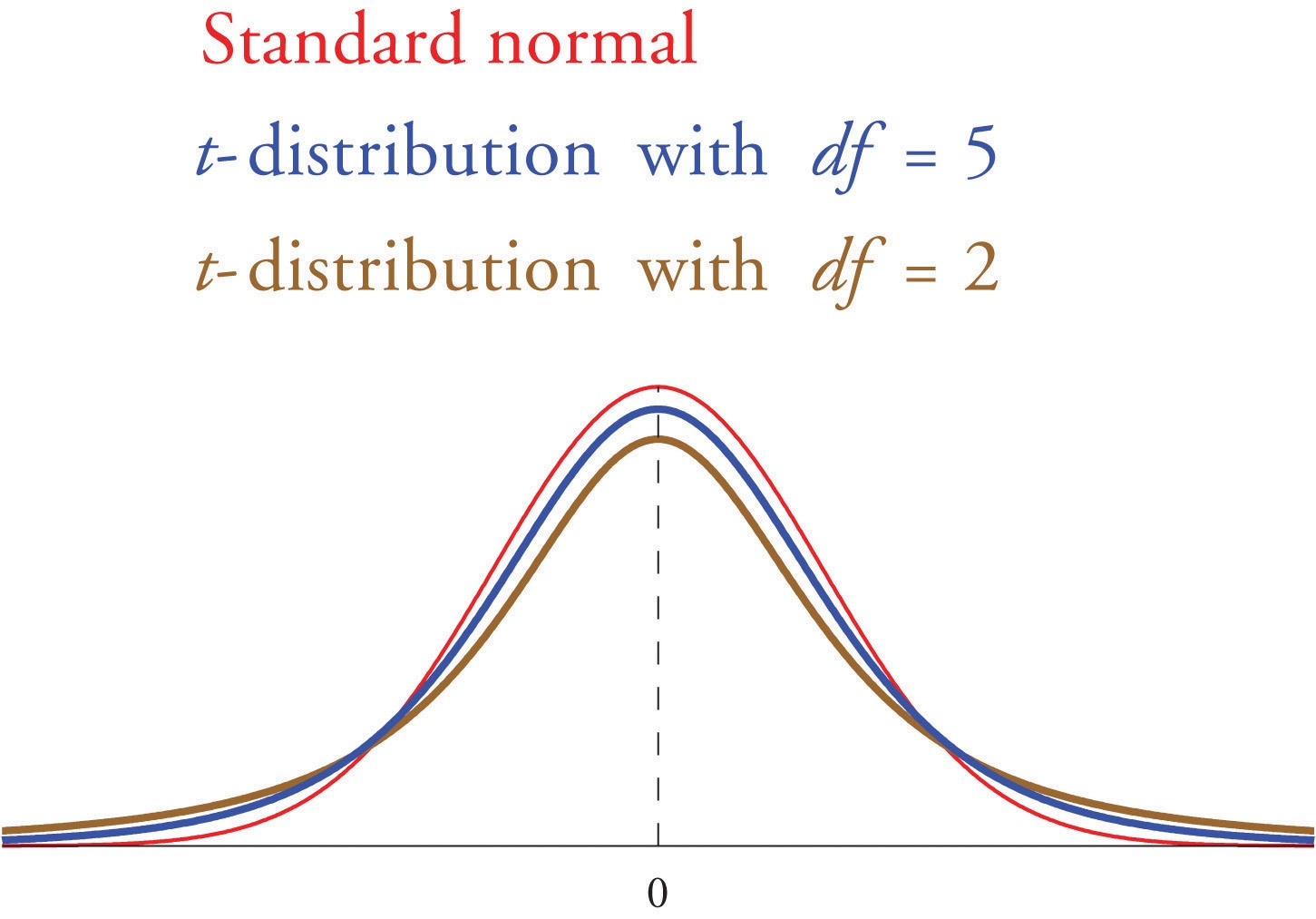
If the population standard deviation is unknown and the sample size n is small then when we substitute the sample standard deviation s for σ the normal approximation is no longer valid. The solution is to use a different distribution, called Student’s t-distribution with $(n−1)$ degrees of freedom. Student’s t-distribution is very much like the standard normal distribution in that it is centered at 0 and has the same qualitative bell shape, but it has heavier tails than the standard normal distribution does, as indicated by Figure "Student’s ", in which the curve (in brown) that meets the dashed vertical line at the lowest point is the t-distribution with two degrees of freedom, the next curve (in blue) is the t-distribution with five degrees of freedom, and the thin curve (in red) is the standard normal distribution. As also indicated by the figure, as the sample size $n$ increases, Student’s t-distribution ever more closely resembles the standard normal distribution. Although there is a different t-distribution for every value of $n$ , once the sample size is 30 or more it is typically acceptable to use the standard normal distribution instead, as we will always do in this text.

Student’s t-Distribution

Just as the symbol $z_c$ stands for the value that cuts off a right tail of area $c$ in the standard normal distribution, so the symbol $t_c$ stands for the value that cuts off a right tail of area $c$ in the standard normal distribution. This gives us the following confidence interval formulas.

Small Sample $100(1−α)\%$ Confidence Interval for a Population Mean

If $σ$ is known: $\bar{x}±z_{α∕2}(σ/\sqrt{n})$

If $σ$ is unknown: $\bar{x}±t_{α∕2}(s/\sqrt{n})$  (degrees of freedom $df=(n−1)$ )

The population must be normally distributed.

A sample is considered small when $n < 30$ .

To use the new formula we use the line in Figure 12.3 "Critical Values of " that corresponds to the relevant sample size.

EXAMPLE 5. A sample of size 15 drawn from a normally distributed population has sample mean 35 and sample standard deviation 14. Construct a 95% confidence interval for the population mean, and interpret its meaning.

[ Solution ]

Since the population is normally distributed, the sample is small, and the population standard deviation is unknown, the formula that applies is $\bar{x} ±t_{α∕2} \frac {s} { \sqrt{n}}$.

Confidence level 95% means that $α=1−0.95=0.05$ so $α∕2=0.025$ . Since the sample size is $n = 15$ , there are $n−1=14$ degrees of freedom. By Figure 12.3 "Critical Values of " $t_{0.025} =2.145$ . Thus $\bar{x} ± t_{α∕2} \frac {s} { \sqrt{n}} = 35 ± 2.145 ( \frac {14}{\sqrt {15} } )=35±7.8$ .

One may be 95% confident that the true value of $μ$ is contained in the interval $(35−7.8,35+7.8)=(27.2,42.8)$ .

R Source

n <- 15
mu <- 35
sd <- 14
alpha <- 0.05

se <- sd / sqrt(n)
t <- qt(1-alpha/2, n-1); t

ll <- mu - t * se
ul <- mu + t * se
ll   # lower limit
ul   # upper limit

Result

> t <- qt(1-alpha/2, n-1); t
## [1] 2.144787
> 
> ll <- mu - t * se
> ul <- mu + t * se
> ll   # lower limit
## [1] 27.24706
> ul   # upper limit
## [1] 42.75294

• Using Rstat Package : pmean.ci2()

R Source

library(Rstat)

pmean.ci2(xb=35, sig=14, n=15, alp=0.05, dig=3)

Result

> pmean.ci2(xb=35, sig=14, n=15, alp=0.05, dig=3)
## [35 ± 2.145×14/√15] = [35 ± 7.753] = [27.247, 42.7]

EXAMPLE 6. A random sample of 12 students from a large university yields mean GPA 2.71 with sample standard deviation 0.51. Construct a 90% confidence interval for the mean GPA of all students at the university. Assume that the numerical population of GPAs from which the sample is taken has a normal distribution.

[ Solution ]

Since the population is normally distributed, the sample is small, and the population standard deviation is unknown, the formula that applies is $\bar{x} ±t_{α∕2} \frac {s} { \sqrt{n}}$ .

Confidence level 95% means that $α=1−0.90=0.10$ so $α∕2=0.05$. Since the sample size is $n = 12$ , there are $n−1=11$ degrees of freedom. By Figure 12.3 "Critical Values of " $t_{0.05} =1.796$ . Thus $\bar{x} ± t_{α∕2} \frac {s} { \sqrt{n}} = 2.71 ± 1.796 ( \frac {0.51}{\sqrt {12} } )=2.71±0.26$ .

One may be 95% confident that the true value of $μ$ is contained in the interval $(2.71−0.26, 2.71+0.26)=(2.45,2.97)$.

R Source

n <- 12
mu <- 2.71
sd <- 0.51
alpha <- 0.10

se <- sd / sqrt(n)
t <- qt(1-alpha/2, n-1); t

ll <- mu - t * se
ul <- mu + t * se
ll   # lower limit
ul   # upper limit

Result

> t <- qt(1-alpha/2, n-1); t
## [1] 1.795885
> 
> ll <- mu - t * se
> ul <- mu + t * se
> ll   # lower limit
## [1] 2.445602
> ul   # upper limit
## [1] 2.974398

• Using Rstat Package : pmean.ci2()

R Source

library(Rstat)

pmean.ci2(xb=2.71, sig=0.51, n=12, alp=0.10, dig=3)

Result

> pmean.ci2(xb=2.71, sig=0.51, n=12, alp=0.10, dig=3)
## [2.71 ± 1.796×0.51/√12] = [2.71 ± 0.264] = [2.446, 2.974]