11-4. F-Tests in One-Way ANOVA

In Chapter 9 "Two-Sample Problems" we saw how to compare two population means $μ_1$ and $μ_2$ . In this section we will learn to compare three or more population means at the same time, which is often of interest in practical applications. For example, an administrator at a university may be interested in knowing whether student grade point averages are the same for different majors. In another example, an oncologist may be interested in knowing whether patients with the same type of cancer have the same average survival times under several different competing cancer treatments.

In general, suppose there are K normal populations with possibly different means, $μ_1,μ_2, … ,μ_K$ , but all with the same variance $σ^2$ . The study question is whether all the K population means are the same. We formulate this question as the test of hypotheses

$H_0:μ_1=μ_2= ⋅ ⋅ ⋅ =μ_K$ vs. $Ha: not all K population means are equal$

To perform the test K independent random samples are taken from the K normal populations. The K sample means, the K sample variances, and the K sample sizes are summarized in the table:

Population

Sample Size

Sample Mean

Sample Variance

$n_1$

$\bar{x_1}$

$s_1^2$

$n_2$

$\bar{x_2}$

$s_2^2$

⋮

$n_k$

$\bar{x_k}$

$s_k^2$

Define the following quantities:

The combined sample size: $n=n_1+n_2+ ⋅ ⋅ ⋅ +n_K$
The mean of the combined sample of all n observations:
$\bar{x} = \frac{Σx}{n}=\frac{ n_1 \bar{x_1} +n_2 \bar{x_2}+ ⋅ ⋅ ⋅ + n_k \bar{x_k} } {n}$
The mean square for treatment:
$MST=\frac{ n_1 (\bar{x_1} - \bar{x})^2 +n_2 (\bar{x_2} - \bar{x})^2+ ⋅ ⋅ ⋅ + n_k (\bar{x_k} - \bar{x})^2 } {K-1}$
The mean square for error:
$MSE= \frac{(n_1−1)s^2_1+(n_2−1)s^2_2+ ⋅ ⋅ ⋅ +(n_K−1)s^2_k}{n-K}$

MST can be thought of as the variance between the K individual independent random samples and MSE as the variance within the samples. This is the reason for the name “analysis of variance,” universally abbreviated ANOVA.

The adjective “one-way” has to do with the fact that the sampling scheme is the simplest possible, that of taking one random sample from each population under consideration.

If the means of the K populations are all the same then the two quantities MST and MSE should be close to the same, so the null hypothesis will be rejected if the ratio of these two quantities is significantly greater than 1.

This yields the following test statistic and methods and conditions for its use.

Test Statistic for Testing the Null Hypothesis that K Population Means Are Equal
$F=\frac{MST}{MSE}$
If the K populations are normally distributed with a common variance and if $H_0:μ_1=μ_2= ⋅ ⋅ ⋅ =μ_K$ is true then under independent random sampling F approximately follows an F-distribution with degrees of freedom $df_1=(K−1)$ and $df_2=(n-K)$ .
The test is right-tailed: $H_0$ is rejected at level of significance αα if $F≥F_α$ .

As always the test is performed using the usual five-step procedure.

EXAMPLE 8. The average of grade point averages (GPAs) of college courses in a specific major is a measure of difficulty of the major. An educator wishes to conduct a study to find out whether the difficulty levels of different majors are the same. For such a study, a random sample of major grade point averages (GPA) of 11 graduating seniors at a large university is selected for each of the four majors mathematics, English, education, and biology. The data are given in Table 11.17 "Difficulty Levels of College Majors". Test, at the 5% level of significance, whether the data contain sufficient evidence to conclude that there are differences among the average major GPAs of these four majors.

TABLE 11.17 DIFFICULTY LEVELS OF COLLEGE MAJORS

Mathematics	English	Education	Biology
2.59	3.64	4.00	2.78
3.13	3.19	3.59	3.51
2.97	3.15	2.80	2.65
2.50	3.78	2.39	3.16
2.53	3.03	3.47	2.94
3.29	2.61	3.59	2.32
2.53	3.20	3.74	2.58
3.17	3.30	3.77	3.21
2.70	3.54	3.13	3.23
3.88	3.25	3.00	3.57
2.64	4.00	3.47	3.22

[ Solution ]

Step 1. The test of hypotheses is $H_0:μ_1=μ_2=μ_3=μ_4$ vs. $H_a: not all four population means are equal$ $@ α=0.05$
Step 2. The test statistic is $F=\frac{MST}{MSE}$ with (since n = 44 and K = 4) degrees of freedom $df1=(K−1)=(4−1)=3$ and $df2=(n−K)=(44−4)=40$ .

Step 3. If we index the population of mathematics majors by 1, English majors by 2, education majors by 3, and biology majors by 4, then the sample sizes, sample means, and sample variances of the four samples in Table 11.17 "Difficulty Levels of College Majors" are summarized (after rounding for simplicity) by:

Major

Sample Size

Sample Mean

Sample Variance

Mathematics

$n_1=11$

$\bar{x_1}=2.90$

$s^2_1=0.188$

English

$n_2=11$

$\bar{x_2}=3.34$

$s^2_2=0.148$

Education

$n_3=11$

$\bar{x_3}=3.36$

$s^2_3=0.229$

Biology

$n_4=11$

$\bar{x_4}=3.02$

$s^2_4=0.157$

The average of all 44 observations is (after rounding for simplicity) $\bar{x}=3.15$ . We compute (rounding for simplicity) $MST=\frac{11(2.90−3.15)^2+11(3.34−3.15)^2+11(3.36−3.15)^2+11(3.02−3.15)^2} {4−1}$ $= \frac{1.75563}{3}=0.585$

and

$MSE= \frac{(11−1)(0.188)+(11−1)(0.148)+(11−1)(0.229)+(11−1)(0.157)}{44−4}$ $= \frac{7.22}{40} = 0.181$

so that $F=\frac{MST}{MSE}=\frac{0.585}{0.181}=3.232$

Step 4. The test is right-tailed. The single critical value is (since $df_1=3$ and $df_2=40$ ) $F_α=F_{0.05}=2.84$ . Thus the rejection region is $[2.84,∞)$ , as illustrated in Figure 11.12.

Figure 11.12 Note 11.36 "Example 8" Rejection Region

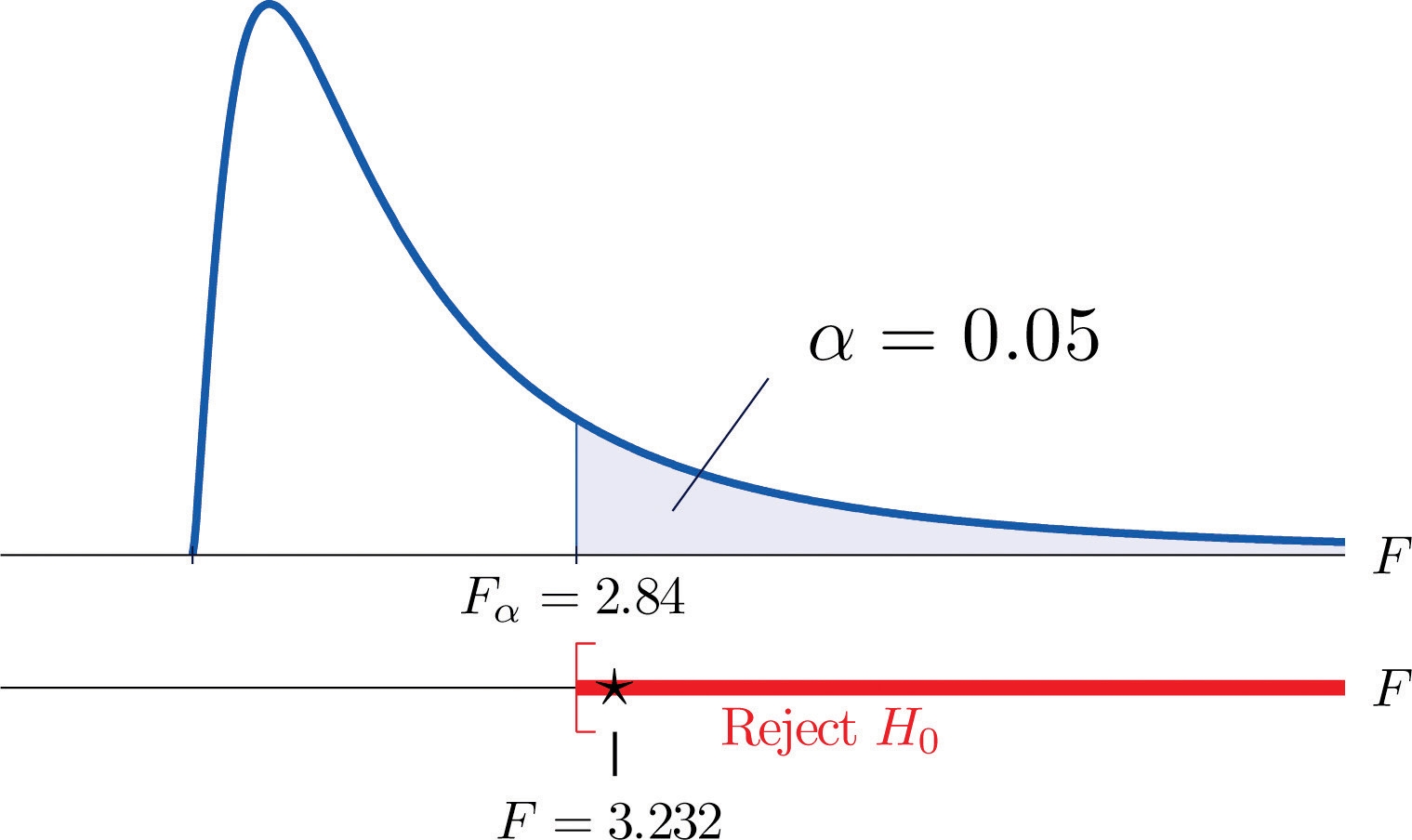
Step 5. Since $F=3.232>2.84$ , we reject $H_0$ .
The data provide sufficient evidence, at the 5% level of significance, to conclude that the averages of major GPAs for the four majors considered are not all equal.

library(Rstat)

y <- c(2.59, 3.13, 2.97, 2.50, 2.53, 3.29, 2.53, 3.17, 2.70, 3.88, 2.64,
       3.64, 3.19, 3.15, 3.78, 3.03, 2.61, 3.20, 3.30, 3.54, 3.25, 4.00,
       4.00, 3.59, 2.80, 2.39, 3.47, 3.59, 3.74, 3.77, 3.13, 3.00, 3.47,
       2.78, 3.51, 2.65, 3.16, 2.94, 2.32, 2.58, 3.21, 3.23, 3.57, 3.22)
f <- c(1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
       2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0,
       3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0,
       4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0, 4.0)

anova1(y, f, xl ="Major", yl = "GPA", step = 0:7)

## [Step 0] Mean of GPA for each level of Major ---------
##      1      2      3      4 
## 2.9027 3.3355 3.3591 3.0155

## [Step 1] Box Plot of GPA for each level of Major ---------

## [Step 2] ANOVA Table of GPA w.r.t. Major ---------
##       Sum Sq. df Mean Sq.     F0 P-value
## Major  1.7305  3   0.5768 3.1992  0.0335
## Error  7.2123 40   0.1803               
## Total  8.9428 43

The value of test statistic = 3.1992
P-value = 0.0335 < α=0.05 ==> reject Ho

## [Step 3] ANOVA Diagnostic Plot of GPA w.r.t. Major ---------

## [Step 4] 95% CI for the Mean of GPA w.r.t. Major ---------
## MSE = 0.1803 
##          1      2      3      4
## ym  2.9027 3.3355 3.3591 3.0155
## tol 0.2588 0.2588 0.2588 0.2588
## lcl 2.6440 3.0767 3.1003 2.7567
## ucl 3.1615 3.5942 3.6178 3.2742

## [Step 5] 95% CI Plot for the Mean of GPA w.r.t. Major ---------

## [Step 6] 95% CI for the Mean Differences of GPA w.r.t. Major ---------
##        A1-A2   A1-A3   A1-A4   A2-A3   A2-A4   A3-A4
## ym2  -0.4327 -0.4564 -0.1127 -0.0236  0.3200  0.3436
## tol2  0.3659  0.3659  0.3659  0.3659  0.3659  0.3659
## lcl2 -0.7987 -0.8223 -0.4787 -0.3896 -0.0459 -0.0223
## ucl2 -0.0668 -0.0904  0.2532  0.3423  0.6859  0.7096

## [Step 7] 95% CI Plot for the Mean Differences of GPA w.r.t. Major ---------

EXAMPLE 9

A research laboratory developed two treatments which are believed to have the potential of prolonging the survival times of patients with an acute form of thymic leukemia. To evaluate the potential treatment effects 33 laboratory mice with thymic leukemia were randomly divided into three groups. One group received Treatment 1, one received Treatment 2, and the third was observed as a control group. The survival times of these mice are given in Table 11.18 "Mice Survival Times in Days". Test, at the 1% level of significance, whether these data provide sufficient evidence to confirm the belief that at least one of the two treatments affects the average survival time of mice with thymic leukemia.

TABLE 11.18 MICE SURVIVAL TIMES IN DAYS

Treatment 1		Treatment 2	Control
71	75	77	81
72	73	67	79
75	72	79	73
80	65	78	71
60	63	81	75
65	69	72	84
63	64	71	77
78	71	84	67
		91

[ Solution ]

Step 1. The test of hypotheses is
$H_0:μ_1=μ_2=μ_3$ vs. $H_a: not all four population means are equal$ $@ α=0.01$
Step 2. The test statistic is $F=\frac{MST}{MSE}$ with (since n = 44 and K = 4) degrees of freedom $df1=(K−1)=(3−1)=3$ and $df2=(n−K)=(33−3)=30$ .

Step 3. If we index the population of mice receiving Treatment 1 by 1, Treatment 2 by 2, and no treatment by 3, then the sample sizes, sample means, and sample variances of the three samples in Table 11.18 "Mice Survival Times in Days" are summarized (after rounding for simplicity) by:

Group

Sample Size

Sample Mean

Sample Variance

Treatment 1

$n_1=16$

$\bar{x_1}=69.75$

$s^2_1=34.47$

Treatment 2

$n_2=9$

$\bar{x_2}=77.78$

$s^2_2=52.69$

Control

$n_3=8$

$\bar{x_3}=75.88$

$s^2_3=30.69$

The average of all 33 observations is (after rounding for simplicity) $\bar{x}=73.42$ . We compute (rounding for simplicity) $MST=\frac{16(69.75−73.42)^2+9(77.78−73.42)^2+8(75.88−73.42)^2} {3-1} = \frac{435.00}{2}=217.50$

and $MSE= \frac{(16−1)(34.47)+(9−1)(52.69)+(8−1)(30.69)}{33−3} = \frac{1153.4} {30}= 38.45$

so that $F=\frac{MST}{MSE}=\frac{217.50}{38.45}=5.66$

Step 4. The test is right-tailed. The single critical value is $Fα=F0.01=5.39$ . Thus the rejection region is $[5.39,∞)$ , as illustrated in Figure 11.13.

Figure 11.13 Note 11.37 "Example 9" Rejection Region

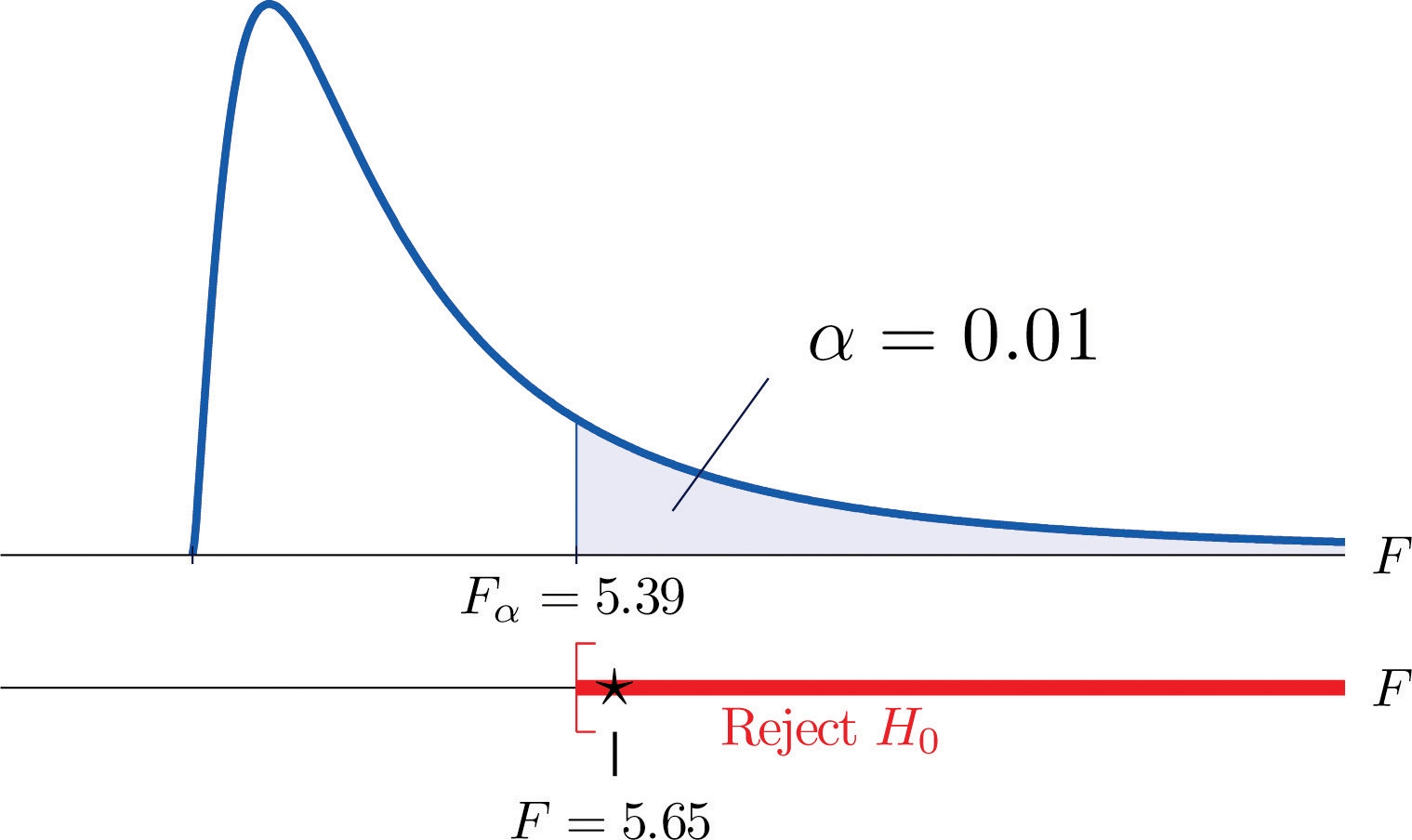
Step 5. Since $F=5.66>5.39$ , we reject $H_0$ .
The data provide sufficient evidence, at the 1% level of significance, to conclude that a treatment effect exists at least for one of the two treatments in increasing the mean survival time of mice with thymic leukemia.

library(Rstat)

y <- c(71, 72, 75, 80, 60, 65, 63, 78, 75, 73, 72, 65, 63, 69, 64, 71,
       77, 67, 79, 78, 81, 72, 71, 84, 91,
       81, 79, 73, 71, 75, 84, 77, 67)
f <- c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       2, 2, 2, 2, 2, 2, 2, 2, 2,
       3, 3, 3, 3, 3, 3, 3, 3)

anova1(y, f, xl ="Treatment & Control", yl = "Survival Times", step = 0:7)

## [Step 0] Mean of Survival Times for each level of Treatment & Control ---------
##       1       2       3 
## 69.7500 77.7778 75.8750 
##

## [Step 1] Box Plot of Survival Times for each level of Treatment & Control ---------
##

## [Step 2] ANOVA Table of Survival Times w.r.t. Treatment & Control ---------
##                       Sum Sq. df Mean Sq.     F0 P-value
## Treatment & Control  434.6301  2  217.315 5.6522  0.0083
## Error               1153.4306 30  38.4477               
## Total               1588.0606 32

F value = 5.6522
P-value = 0.0083 < 0.01 ==> reject Ho

## [Step 3] ANOVA Diagnostic Plot of Survival Times w.r.t. Treatment & Control ---------

## [Step 4] 95% CI for the Mean of Survival Times w.r.t. Treatment & Control ---------
## MSE = 38.4477 
##           1       2       3
## ym  69.7500 77.7778 75.8750
## tol  3.1658  4.2211  4.4772
## lcl 66.5842 73.5567 71.3978
## ucl 72.9158 81.9989 80.3522

## [Step 5] 95% CI Plot for the Mean of Survival Times w.r.t. Treatment & Control ---------

## [Step 6] 95% CI for the Mean Differences of Survival Times w.r.t. Treatment & Control ---------
##         A1-A2    A1-A3   A2-A3
## ym2   -8.0278  -6.1250  1.9028
## tol2   5.2764   5.4834  6.1533
## lcl2 -13.3042 -11.6084 -4.2505
## ucl2  -2.7514  -0.6416  8.0561

[Step 7] 95% CI Plot for the Mean Differences of Survival Times w.r.t. Treatment & Control ---------

It is important to to note that, if the null hypothesis of equal population means is rejected, the statistical implication is that not all population means are equal. It does not however tell which population mean is different from which. The inference about where the suggested difference lies is most frequently made by a follow-up study.

Previous11-3. Exercises Next11-4. Exercises

Last updated 4 years ago