5-4. Areas of Tails of Distributions

密度曲线的尾部

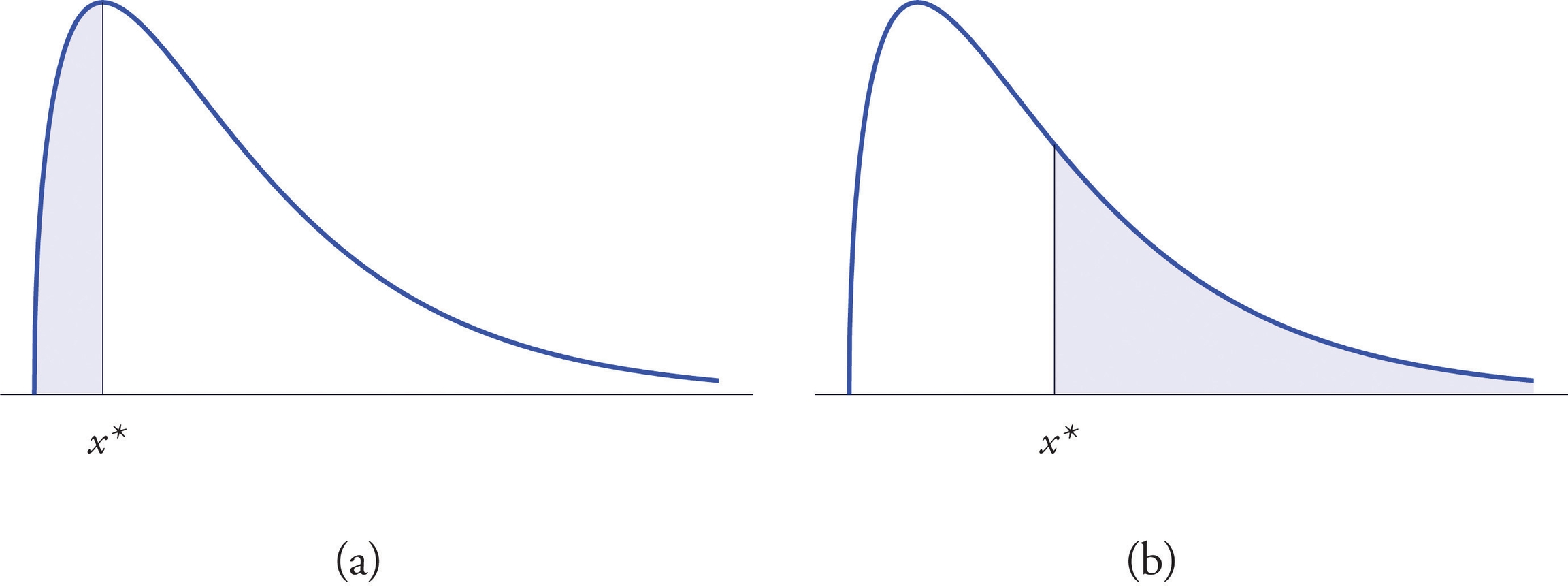
The left tail of a density curve $y=f(x)$ of a continuous random variable X cut off by a value $x^*$ of X is the region under the curve that is to the left of $x^*$ , as shown by the shading in Figure "Right and Left Tails of a Distribution" (a). The right tail cut off by $x^*$ is defined similarly, as indicated by the shading in Figure "Right and Left Tails of a Distribution" (b).

1. Tails of the Standard Normal Distribution

At times it is important to be able to solve the kind of problem illustrated by the figure as follows. We have a certain specific area in mind, in this case the area 0.0125 of the shaded region in the figure, and we want to find the value $z^*$ of $Z$ that produces it. This is exactly the reverse of the kind of problems encountered so far. Instead of knowing a value $z^*$ of $Z$ and finding a corresponding area, we know the area and want to find $z^*.$ In the case at hand, in the terminology of the definition just above, we wish to find the value $z^*$ that cuts off a left tail of area 0.0125 in the standard normal distribution.

Z Value that Produces a Known Area 0.0125

EXAMPLE 17. Find the value $z^*$ of $Z$ as determined by the above figure: the value $z^*$ that cuts off a left tail of area 0.0125 in the standard normal distribution. In symbols, find the number $z^*$ such that $P(Z<z^*)=0.0125.$

[ Solution ]

R Code

qnorm(0.0125)

z*

Plot

EXAMPLE 18. Find the value $z^*$of $Z$ as determined by Figure : the value $z^*$ that cuts off a right tail of area 0.0250 in the standard normal distribution. In symbols, find the number $z^*$ such that $P(Z>z^*)=0.0250.$

[ Solution ]

• The value of the standard normal random variable $Z$ that cuts off a right tail of area c is denoted $z_c$ . By symmetry, value of $Z$ that cuts off a left tail of area c is $−z_c.$ See the below "The Numbers ".

R Code

qnorm(0.9750)

z*

Plot

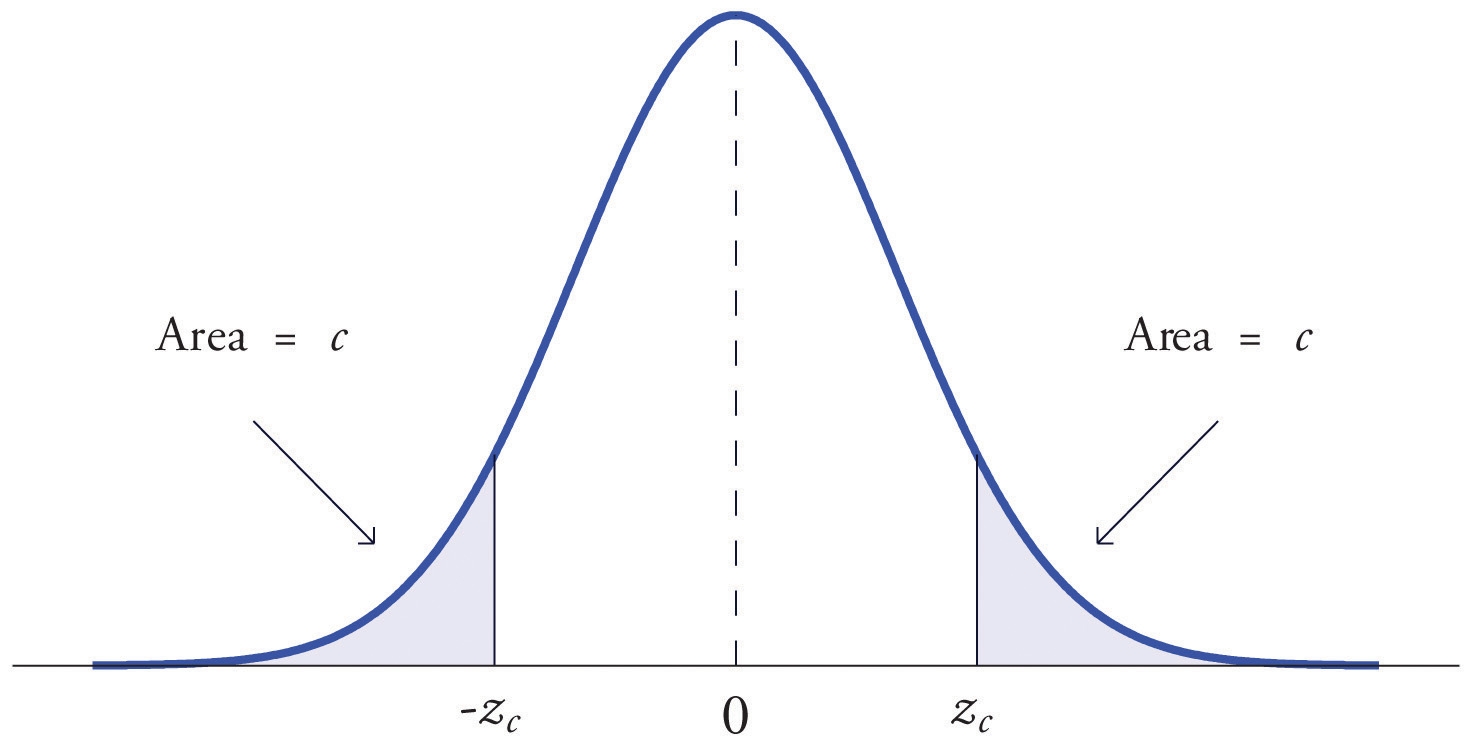
EXAMPLE 19. Find $z_{.01}$ and $−z_{.01}$ , the values of $Z$ that cut off right and left tails of area 0.01 in the standard normal distribution.

[ Solution ]

R Code

qnorm(0.99)

z*

Plot

2. Tails of General Normal Distributions

Suppose $X$ is a normally distributed random variable with mean $μ$ and standard deviation $σ$ . To find the value $x^*$ of $X$ that cuts off a left or right tail of area c in the distribution of $X$ :

1. find the value $z^*$ of $Z$ that cuts off a left or right tail of area c in the standard normal distribution;

2. $z^*$ is the z-score of $x^*$; compute $x^*$ using the destandardization formula $x^*=μ+z^* σ$

EXAMPLE 20. Find $x^*$ such that $P(X<x*)=0.9332$ , where $X$ is a normal random variable with mean $μ = 10$ and standard deviation $σ = 2.5$ .

[ Solution ]

R Code

qnorm(0.9332, mean=10, sd=2.5)

x*

Plot

EXAMPLE 21. Find $x^*$ such that $P(X>x^*)=0.65$ , where X is a normal random variable with mean $μ = 175$ and standard deviation $σ = 12$ .

[ Solution ]

R Code

qnorm(1-0.65, mean=175, sd=12)

x*

Plot

EXAMPLE 22. Scores on a standardized college entrance examination (CEE) are normally distributed with mean 510 and standard deviation 60. A selective university decides to give serious consideration for admission to applicants whose CEE scores are in the top 5% of all CEE scores. Find the minimum score that meets this criterion for serious consideration for admission.

[ Solution ]

R Code

qnorm(1-0.05, mean=510, sd=60)

x*

Plot

EXAMPLE 23. All boys at a military school must run a fixed course as fast as they can as part of a physical examination. Finishing times are normally distributed with mean 29 minutes and standard deviation 2 minutes. The middle 75% of all finishing times are classified as “average.” Find the range of times that are average finishing times by this definition.

[ Solution ]

R Code

a <- qnorm(0.125, mean=29, sd=2) ; a
b <- qnorm(1-0.125, mean=29, sd=2) ; b

x*

Plot

3. Using qnorm() and pnormGC in R

$X$~ $norm(\mu, \sigma)$

1) find $z^*$ or $x^*$

qnorm(p, mean = , sd = )

2) plotting (See 5-3. pnormGC())

pnormGC(p, region= , mean=, sd =, graph = )

EXAMPLE 24. $P(Z<z^*)=0.0125.$

R Code

qnorm(0.0125)

z*

R Code

Plot

EXAMPLE 25. Find $x^*$ such that $P(X<x*)=0.9332$ , where $X$ is a normal random variable with mean $μ = 10$ and standard deviation $σ = 2.5$ .

R Code

x <- qnorm(0.9332, mean=10, sd=2.5); x <- round(x, 2); x
pnormGC(x, region = "below", mean=10, sd=2.5, graph=TRUE)

x*

Plot

密度曲线的尾部 tail of a density curve 一般正态分布 General Normal Distributions