9-4. Comparison of Two Population Proportions

Suppose we wish to compare the proportions of two populations that have a specific characteristic, such as the proportion of men who are left-handed compared to the proportion of women who are left-handed.

Figure 9.7 "Independent Sampling from Two Populations In Order to Compare Proportions" illustrates the conceptual framework of our investigation. Each population is divided into two groups, the group of elements that have the characteristic of interest (for example, being left-handed) and the group of elements that do not. We arbitrarily label one population as Population 1 and the other as Population 2, and subscript the proportion of each population that possesses the characteristic with the number 1 or 2 to tell them apart.

We draw a random sample from Population 1 and label the sample statistic it yields with the subscript 1. Without reference to the first sample we draw a sample from Population 2 and label its sample statistic with the subscript 2.

Figure 9.7 Independent Sampling from Two Populations In Order to Compare Proportions

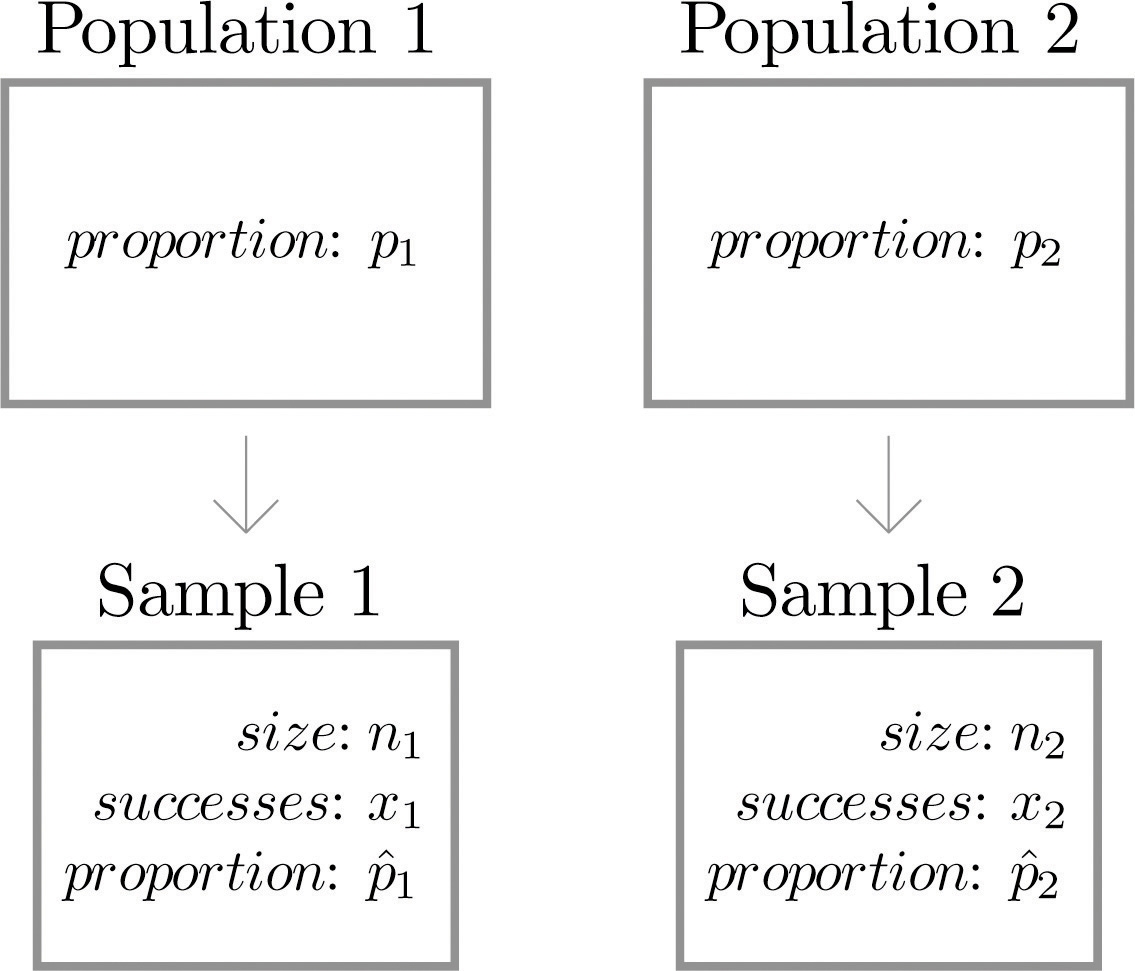
Our goal is to use the information in the samples to estimate the difference $p_1−p_2$ in the two population proportions and to make statistically valid inferences about it.

1. Confidence Intervals

Since the sample proportion $\hat{p_1}$ computed using the sample drawn from Population 1 is a good estimator of population proportion p1 of Population 1 and the sample proportion $\hat{p_2}$ computed using the sample drawn from Population 2 is a good estimator of population proportion $p_2$ of Population 2, a reasonable point estimate of the difference $(p_1−p_2)$ is $(\hat{p_1}−\hat{p_2}).$

In order to widen this point estimate into a confidence interval we suppose that both samples are large, as described in Section 7.3 "Large Sample Estimation of a Population Proportion" in Chapter 7 "Estimation" and repeated below. If so, then the following formula for a confidence interval for $(p_1−p_2)$ is valid.

$100(1−α)\%$ Confidence Interval for the Difference Between Two Population Proportions

$(\hat{p_1}−\hat{p_2})±z_{α∕2} \sqrt{ \frac{ \hat{p_1}(1−\hat{p_1})}{n_1}+ \frac{\hat{p_2}(1−\hat{p_2})}{n_2} }$

The samples must be independent, and each sample must be large: each of the intervals $[\hat{p_1} − 3 \sqrt{ \frac{\hat{p_1}(1−\hat{p_1})}{n_1}}, \hat{p_1} + 3 \sqrt{ \frac{\hat{p_1}(1−\hat{p_1})}{n_1}}]$

and

$[\hat{p_2} − 3 \sqrt{ \frac{\hat{p_2}(1−\hat{p_2})}{n_2}}, \hat{p_2} + 3 \sqrt{ \frac{\hat{p_2}(1−\hat{p_2})}{n_2}}]$

must lie wholly within the interval $[0,1].$

EXAMPLE 10. The department of code enforcement of a county government issues permits to general contractors to work on residential projects. For each permit issued, the department inspects the result of the project and gives a “pass” or “fail” rating. A failed project must be re-inspected until it receives a pass rating. The department had been frustrated by the high cost of re-inspection and decided to publish the inspection records of all contractors on the web. It was hoped that public access to the records would lower the re-inspection rate. A year after the web access was made public, two samples of records were randomly selected. One sample was selected from the pool of records before the web publication and one after. The proportion of projects that passed on the first inspection was noted for each sample. The results are summarized below. Construct a point estimate and a 90% confidence interval for the difference in the passing rate on first inspection between the two time periods. No public web access : $n_1=500, \hat{p_1}=0.67$ Public web access : $n_2=100, \hat{p_1}=0.80$

[ Solution ]

The point estimate of $(p_1−p_2)$ is $(\hat{p_1}−\hat{p_2}) = =0.67−0.80=−0.13.$

Because the “No public web access” population was labeled as Population 1 and the “Public web access” population was labeled as Population 2, in words this means that we estimate that the proportion of projects that passed on the first inspection increased by 13 percentage points after records were posted on the web.

The sample sizes are sufficiently large for constructing a confidence interval since for sample 1: $3 \sqrt{ \frac{\hat{p_1}(1−\hat{p_1})}{n_1}} = 3 \sqrt{\frac{(0.67)(0.33)}{500}} = 0.06$

so that

$[\hat{p_1} − 3 \sqrt{ \frac{\hat{p_1}(1−\hat{p_1})}{n_1}}, \hat{p_1} + 3 \sqrt{ \frac{\hat{p_1}(1−\hat{p_1})}{n_1}}]$ $=[0.67−0.06,0.67+0.06 ]$ $=[0.61,0.73 ]⊂[0,1 ]$

and for sample 2:

$3\sqrt{ \frac{\hat{p_2}(1−\hat{p_2})}{n_2}} = 3 \sqrt{ \frac{ (0.8)(0.2)}{100}} =0.12$

so that

$[\hat{p_2} − 3 \sqrt{ \frac{\hat{p_2}(1−\hat{p_2})}{n_2}}, \hat{p_2} + 3 \sqrt{ \frac{\hat{p_2}(1−\hat{p_2})}{n_2}}]$ $=[0.8−0.12,0.8+0.12 ]$ $=[0.68,0.92 ]⊂[0,1 ]$

To apply the formula for the confidence interval, we first observe that the 90% confidence level means that $α=(1−0.90)=0.10$ so that $z_{α∕2}=z_{0.05}.$ From Figure 12.3 "Critical Values of " we read directly that $z_{0.05}=1.645.$

Thus the desired confidence interval is

$(\hat{p_1}−\hat{p_2})±z_{α∕2} \sqrt{ \frac{ \hat{p_1}(1−\hat{p_1})}{n_1}+ \frac{\hat{p_2}(1−\hat{p_2})}{n_2} }$ $= −0.13±1.645 \sqrt{ \frac{(0.67)(0.33)}{500}+\frac{(0.8)(0.2)}{100} }$ $= −0.13±0.07$

The 90% confidence interval is $[−0.20,−0.06 ].$

We are 90% confident that the difference in the population proportions lies in the interval $[−0.20,−0.06 ]$, in the sense that in repeated sampling 90% of all intervals constructed from the sample data in this manner will contain $p_1−p_2.$

Taking into account the labeling of the two populations, this means that we are 90% confident that the proportion of projects that pass on the first inspection is between 6 and 20 percentage points higher after public access to the records than before.

2. Hypothesis Testing

In hypothesis tests concerning the relative sizes of the proportions $p_1$ and $p_2$ of two populations that possess a particular characteristic, the null and alternative hypotheses will always be expressed in terms of the difference of the two population proportions. Hence the null hypothesis is always written $H_0:p_1−p_2=D_0$

The three forms of the alternative hypothesis, with the terminology for each case, are:

Form of HaHa	Terminology
$H_a:p_1−p_2<D_0$	Left-tailed
$H_a:p_1−p_2>D_0$	Right-tailed
$H_a:p_1−p_2 \ne D_0$	Two-tailed

As long as the samples are independent and both are large the following formula for the standardized test statistic is valid, and it has the standard normal distribution.

Standardized Test Statistic for Hypothesis Tests Concerning the Difference Between Two Population Proportions

$z_o= \frac {(\hat{p_1}−\hat{p_2})−D_0} { \sqrt{ \frac{ \hat{p_1}(1−\hat{p_1})}{n_1} + \frac{\hat{p_2}(1−\hat{p_2})}{n_2} } }$

The test statistic has the standard normal distribution.

The samples must be independent, and each sample must be large: each of the intervals

$[\hat{p_1} − 3 \sqrt{ \frac{\hat{p_1}(1−\hat{p_1})}{n_1}}, \hat{p_1} + 3 \sqrt{ \frac{\hat{p_1}(1−\hat{p_1})}{n_1}}]$

and

$[\hat{p_2} − 3 \sqrt{ \frac{\hat{p_2}(1−\hat{p_2})}{n_2}}, \hat{p_2} + 3 \sqrt{ \frac{\hat{p_2}(1−\hat{p_2})}{n_2}}]$

must lie wholly within the interval $[0,1].$

EXAMPLE 11. Using the data of Note 9.25 "Example 10", test whether there is sufficient evidence to conclude that public web access to the inspection records has increased the proportion of projects that passed on the first inspection by more than 5 percentage points. Use the critical value approach at the 10% level of significance.

[ Solution ]

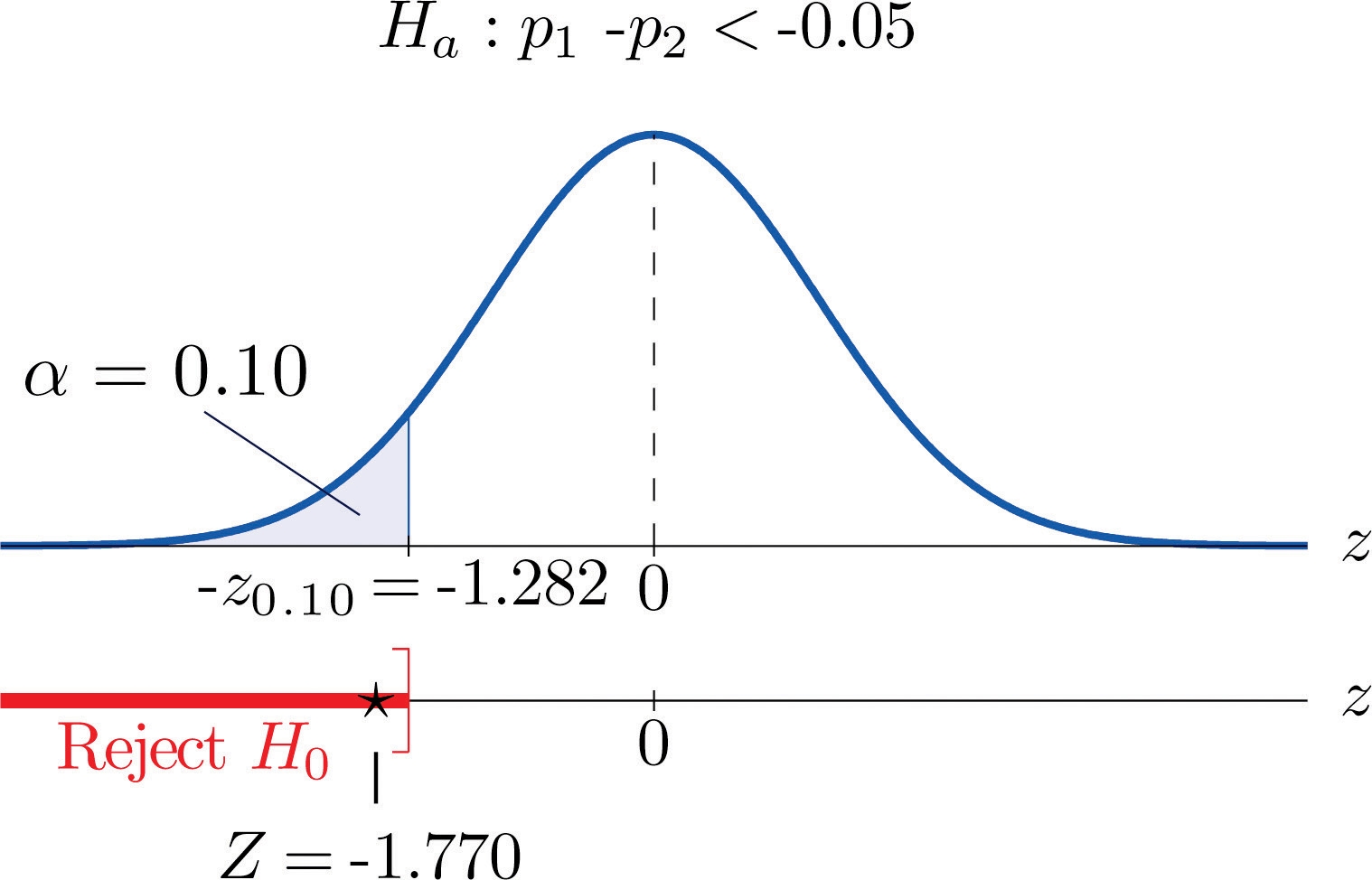
• Step 1. the hypothesis test is $H_0:p_1−p_2=-0.05  vs. H_a:p_1−p_2<−0.05, @  α=0.10$
• Step 2. Since the test is with respect to a difference in population proportions the test statistic is $z_o= \frac {(\hat{p_1}−\hat{p_2})−D_0} { \sqrt{ \frac{ \hat{p_1}(1−\hat{p_1})}{n_1} + \frac{\hat{p_2}(1−\hat{p_2})}{n_2} } }$
• Step 3. Inserting the values given in Note 9.25 "Example 10" and the value $D_0=−0.05$ into the formula for the test statistic gives $Z= \frac {(\hat{p_1}−\hat{p_2})−D_0} { \sqrt{ \frac{ \hat{p_1}(1−\hat{p_1})}{n_1} + \frac{\hat{p_2}(1−\hat{p_2})}{n_2} } }$

  $= \frac {(−0.13)−(−0.05)} {\sqrt { \frac {(0.67)(0.33)}{500}+ \frac{(0.8)(0.2)}{100}}} = −1.770$
• Step 4. Since the symbol in $H_a$ is “ $<$ ” this is a left-tailed test, so there is a single critical value, $z_α=−z_{0.10}.$ From the last row in Figure 12.3 "Critical Values of " $z_{0.10}=1.282$ , so $−z_{0.10}=−1.282.$ The rejection region is $(−∞,−1.282 ].$
• Step 5. As shown in Figure 9.8 "Rejection Region and Test Statistic for " the test statistic falls in the rejection region. The decision is to reject $H_0$ .
• In the context of the problem our conclusion is:

  The data provide sufficient evidence, at the 10% level of significance, to conclude that the rate of passing on the first inspection has increased by more than 5 percentage points since records were publicly posted on the web.

Figure 9.8 Rejection Region and Test Statistic for Note 9.27 "Example 11"

EXAMPLE 12. Perform the test of Note 9.27 "Example 11" using the p-value approach.

[ Solution ]

• Step 4. Because the test is left-tailed the observed significance or p-value of the test is just the area of the left tail of the standard normal distribution that is cut off by the test statistic $z_o=−1.770.$ From Figure 12.2 "Cumulative Normal Probability" the area of the left tail determined by −1.77 is 0.0384. The p-value is 0.0384.
• Step 5. Since the p-value 0.0384 is less than $α=0.10.$ , the decision is to reject the null hypothesis: The data provide sufficient evidence, at the 10% level of significance, to conclude that the rate of passing on the first inspection has increased by more than 5 percentage points since records were publicly posted on the web.

Finally a common misuse of the formulas given in this section must be mentioned. Suppose a large pre-election survey of potential voters is conducted. Each person surveyed is asked to express a preference between, say, Candidate A and Candidate B. (Perhaps “no preference” or “other” are also choices, but that is not important.) In such a survey, estimators $\hat{p_A}$ and $\hat{p_B}$ of $p_A$ and $p_B$ can be calculated. It is important to realize, however, that these two estimators were not calculated from two independent samples. While $\hat{p_A} - \hat{p_B}$ may be a reasonable estimator of $p_A - p_B$ the formulas for confidence intervals and for the standardized test statistic given in this section are not valid for data obtained in this manner.